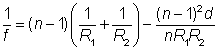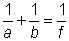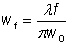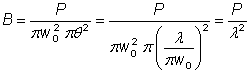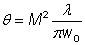LED glass lens /Glass lens street light/Floodlight
  • 0

    No products in the cart.

Tag LED模组

高斯光束(Gaussian beams)

定义：光束在垂直于光轴平面上的电场可由高斯方程表示，有时还会有附加的抛物线型相位曲线。

相关词条：模式ABCD矩阵光束参量乘积光束质量光束半径束腰准直光束衍射极限光束古依相移激光光束M2因子

尤其是在激光物理中，激光光束通常为高斯光束，是以数学家和物理学家Johann Carl Friedrich Gauß命名。这时功率为P的光束光强的横断面可由高斯方程表示： 

1.png

这里光束半径w(z)为光强降为峰值的1/e2 (≈ 13.5%)时距光轴的距离。孔径半径为w时可以透射约86.5%的光功率。如果孔径半径为1.5w或者2w，传输比例分别提高到 98.9%和99.97%。 

除了强度可以采用高斯方程描述，高斯光束的横向相位曲线可由最多二阶多项式来描述。在一个方向上相位的线性变化可由一个倾角描述，相位的二阶变化则与光束的发散和会聚相关。 

目录

  1. 高斯光束的传输
  2. 复数参数
  3. 像散光束
  4. 高斯光束和谐振腔模式
  5. 高斯光束的重要性

高斯光束的传输 

通常在傍轴近似适用的情况下将光束看做高斯光束，即光束发散角比较小。这一近似下，传播方程中的二阶导数项可以忽略，只得到一阶微分方程。并且采用这种近似时，高斯光束在自由空间中传播仍然保持高斯型，其参数会发生一些变化。一束单色光束，波长为 λ，在z轴传播时，电场的复振幅为： 

1.png

最大幅值为|E0|，束腰处的光束半径为 w0，波数 k = 2π / λ，zR为瑞利长度，波前的曲率半径为R(z)。震荡的实数电场可以通过乘以相位因子exp(i 2π c t / λ) 并且取实部得到。 

1.png

图1：高斯光束焦点处的电场分布。这时光束半径比波长稍大，光速发散角很大。根据以上方程，场由左侧向右侧移动。 

在传播方向上的光束半径变化为： 

1.png

其中瑞利长度为： 

1.png

决定了在多长距离范围内光束不会发散很严重的传播。（之前通常采用共焦长b描述，它是瑞利长度的二倍。）准直光束（光束半径接近于常数）的瑞利长度与传播距离相比比较大。 

1.png

图2：高斯光束的光束半径变化（蓝色曲线）。两条竖线代表瑞利长度，虚线表明远离束腰的渐变变化情况。 

以上方程中 z = 0对应于束腰或者焦点，在该点光束半径是最小的，相位曲线是平坦的。波前曲率半径为R的演化遵循方程： 

1.png

在透明介质中传播时，λ是介质中的波长（非真空波长）。上面采用的其它参数和方程都不用改变，这时假设了介质是各向同性、均匀和无损耗的。 

1.png

图3：具有弯曲波前的高斯光束。在接近于焦点和远离焦点时曲率都很小。 电场中的反正切项对应的是古依相移，对于光学谐振腔的谐振频率非常重要。 

远场的光束发散角为： 

1.png

表明束腰半径越小，波长越长，则远离束腰后光束的发散越强。高斯光束的光束参数乘积（束腰半径与远场发散角的乘积）等于 λ/π，只与波长有关。如果激光光束的光束质量是非理想的，该值会更大。 

傍轴近似需要焦点处光束半径比波长大。这表明这时光束发散角不会很大，并且瑞利长度远大于光束半径。紧聚焦光束一般不能很好的满足傍轴近似，这时需要更加复杂的方法来计算光束传播情况。 

复数参数 

在z处高斯光束的状态可以由一个复数q表征： 

1.png

这样复电场可写为： 

1.png

传输一定距离可以简单的表示为该距离上q参数的增加。当高斯光束通过一个曲面镜或者透镜时， q参数变化可由ABCD矩阵表示： 

1.png

像散光束 

在两垂直的横平面方向上，写为x和y方向，高斯光束的半径和发散角可能不同。上面给出的方程可分别用来描述每一方向上光束半径的变化。如果两个方向上的焦点位置不重合，就称该光束是像散的。 

高斯光束和谐振腔模式 

如果谐振腔是稳定的，谐振腔中的光学介质是各项同性的，介质表面要么是平坦的或者是抛物线形状的，那么光学谐振腔横向的最低阶模式（TEM00或者横向基模）就是高斯模。因此，只辐射横向基模的激光器辐射的光束接近于高斯型。而任何偏离之前描述的条件，例如，增益介质中存在热透镜效应等，都会使光束为非高斯型，同时还会激发多个纵模。更高阶纵模可由厄米-高斯方程或者拉盖尔-高斯方程来描述。任意情况下，与高斯谱型的偏离都可以由 M2因子定量表示。高斯光束具有最高的光束质量，对应的光束参量乘积最小，并且对应的M2 = 1。 

光纤的基模并不严格为高斯型，但是形状与高斯型差别不是很大。因此，采用合适的光学元件，高斯光束可以有效进入单模光纤中（80%或更大）。 

高斯光束的重要性 

高斯光束的重要性体现在以下几个重要特性上： 

  1. 在光轴的任意位置处高斯光束的强度横断面曲线都是高斯型，只是光束半径会发生变化。 
  2. 通过一些简单的光学元件后（例如，无象差透镜）。 
  3. 当腔内不存在光束畸变的情况下，高斯光束为光学谐振腔的最低阶模式（谐振腔模式）。因此许多激光器的输出都是高斯光束。 
  4. 单模光纤中的模式形状接近于高斯型。通常在计算中会采用高斯近似因为这在计算光束传播情况时相对简单。 
  5. 高阶模式对应的是厄米-高斯型。场分布更加复杂，光束参量乘积更大。 
  6. 高斯模式分析可以推广到光束质量差的光束中，需要采用M2因子。 
菲涅尔方程(Fresnel equations)

定义：描述两透明各向同性介质截面处透射系数和反射系数幅值的方程。

菲涅尔方程是描述两透明各向同性介质截面处透射系数和反射系数幅值的方程： 

1.png
1.png

图1：两介质截面处的折射过程 

其中n1 和n2 是两介质的折射率。对应的传播角度（与法线的夹角）为 θ1 和 θ2（见图1）。例如，s偏振（电场矢量与入射平面垂直）透射系数大小为ts。 

功率反射系数是对应反射系数大小的平方。而透射功率系数，考虑到不同的传播角度，需要在前面加一个系数(n2 cos θ2) / (n1 cos θ1)。 

1.png

图2：s和p偏振的功率反射率，采用的折射率为1.45. 

图2给出了界面处功率反射率与入射角度和偏振态的关系。P偏振在入射角为布儒斯特角时（这里约为55.4°）反射系数变为0. 

焦距(focal length)

定义：衡量光学系统聚焦或者使光散焦程度的量。

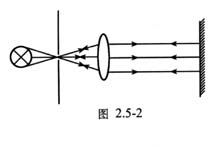
很多类型的光学系统（例如，显微镜吴静和弯曲的激光器反射镜）都可以聚焦或者使光散焦，焦距就是量化这些效应的量。最简单的情形为薄透镜（图1a）。如果入射到透镜的光是一束准直光束，经过透镜后光束会发生聚焦，这时焦距就是从透镜到焦点的距离（假设棱镜是处于真空或者空气中，而不是处于折射率很高的物质中）。而对于散焦透镜（图1b），焦距则是从透镜到虚焦点（采用虚线表示）的距离，是负值。 

1.png

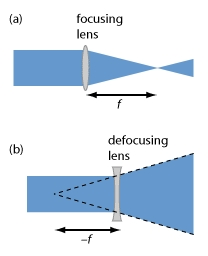
图1：聚焦和散焦透镜的焦距。散焦透镜的焦距为负值。 

目录 

  1. 透镜的焦距
  2. 曲面镜的焦距
  3. 光学系统的焦距
  4. 照相物镜的有效焦距
  5. 焦距可调的光学系统
  6. 与波长有关的焦距
  7. 屈光本领
  8. 发散光束的聚焦
  9. 束腰半径

透镜的焦距 

可以采用下列方程计算透镜的屈光度和焦距，透镜材料的折射率为n，两表面的曲率半径分别为R1和R2： 

1.png

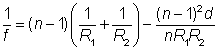
凸面的曲率半径为正数，而凹面的曲率半径则是负值。聚焦透镜得到的结果为正值，结果为负值则对应的为散焦透镜。后面的一项只有当棱镜很厚，两面曲率半径都很大时才需要考虑。 

这一方程适宜于傍轴光线情形，即光线离对称轴不远的情况。 

曲面镜的焦距 

经常采用曲面镜聚焦或者散焦光束。例如，在激光器谐振腔，具有电介质涂层的激光反射镜比普通的透镜更适用，主要是因为反射镜损耗更小。 

当光轴垂直于反射镜表面时，表面曲面半径为R的反射镜的焦距f = R / 2。（正号代表凸面和聚焦反射镜。）如果光轴与表面法线方向夹角 θ 不为0，那么切向（入射平面）的焦距为 ftan = (R / 2) • cos θ，矢状方向的焦距为 fsag = (R / 2) / cos θ 。 

激光反射镜的曲面半径通常在10 mm到5 m之间。如果曲面半径非常小，制备介质涂层会非常困难，但是采用精细的工艺也可以得到仅为几毫米焦距的反射镜，这在一些微型激光器中会用到。 

光学系统的焦距 

一个光学系统可能包含多个透镜和其它光学元件，因此不能采用上面定义的焦距，因为不能明确应计算何处到焦点的距离：是从光学系统的起点、终点、中点还是其它位置？原则上可以采用任意的参考点，但是这时有些原理不能使用，这些原理在具有特定焦距的透镜焦点处光束束腰半径是适用的，或者望远镜的放大倍数等。有人采用前焦距来表示焦点与光学元件的前表面之间的距离。 

照相物镜的有效焦距 

在照相术中，有效焦距具有非常不同的意义，下面我们详细解释一下。 

照相机的视角由胶片上像的尺寸与焦距的比值决定。胶片相机一直采用35 mm胶片（根据ISO标准1007也称为135胶片），胶片上像的尺寸为标准的36 mm × 24 mm。（胶卷轴的宽度为35mm，比24 mm大是为了使图像不会扩展到卷轴的边缘。）这时物镜的焦距为标准的50 mm。然而现在的数码相机（尤其是尺寸小的）通常包含尺寸小于36 mm × 24 mm的像传感器，因此为了得到相同的视场，对应的物镜焦距也比较小（例如32 mm）。许多摄影师仍然习惯采用常用的焦距与视角的比值，因此常用有效焦距来表征数码相机的焦距，此时的焦距数码相机的视场与与普通35 mm胶片的视场相同。例如，实际焦距为32 mm也可以说成标准物镜的有效焦距为50 mm。 

随着越来越少的人采用35 mm胶片，这一转换过程以后可能不会采用。 

焦距可调的光学系统 

在有些系统中，尤其是聚焦成像系统，需要光学系统的焦距是可调的。可以采用下面的原理： 

  • 如果透镜是由可变形的材料做成的，施加机械应力会改变其形状，因此可以改变焦距。这一原理可用于接目镜中。需要聚焦附近的物体时焦距会变短。 
  • 当光学系统包含多个光学元件时（例如，透镜），可以调节光学元件之间的相对距离来调节焦距。这一原理可以用于照相机的变焦物镜中。 

与波长有关的焦距 

普通透镜是利用光的折射，由于折射率与波长有关（色散），因此焦距也与波长相关。这一效应会使成像系统产生色差，在工作于宽波长区域的光学系统中也存在类似的问题。可以设计采用多个透镜（例如，照相机的物镜）来使色差最小化。最常用的做法是采用消色差双合透镜，即由两种材料组成的透镜，这样总体色差很大部分的被抵消了。 

也可以只采用包含反射镜的光学系统来消除色差。曲面半径为R的曲面镜的焦距为 f = R / 2 ，只由几何形状决定，而与波长无关。但是，在非正交入射的情况下，切平面的焦距与入射角余弦成正比，矢状面与入射角余弦的倒数成正比。因此这种系统会产生像散。 

屈光本领 

透镜的屈光本领等于焦距的倒数。表明强聚焦的透镜焦距小，但是屈光本领大。屈光本领的单位为m−1，也称为屈光度（dpt）。对于验光眼镜，常用屈光本领来表征，这时焦距指的是标准透镜，显微镜物镜和照相物镜的焦距。 

很多情况下，屈光本领是比焦距更常用的量。例如，激光晶体中热透镜的屈光本领正比于耗散功率。采用热透镜屈光本领表示的激光器谐振腔稳定区域的宽度与激光晶体的最小模式半径和光波长都有关系，而用焦距表征的稳定区域与参数之间的关系更加复杂。 

发散光束的聚焦 

1.png

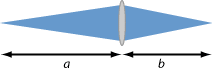
 图2：透镜方程的图解。

发散光束入射到聚焦透镜上时，焦点距离透镜的距离比f大（图2）。透镜方程可写为： 

1.png

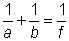
其中a是入射光束的焦点与透镜之间的距离。当a >> f时，有b ≈ f，而其它情况下，则有b > f 。这一关系可以这样直观的理解：使入射光束准直（即消除光束发散）需要聚焦能力为1 / a，这样只需聚焦能力为 1 / f − 1 / a可将光束聚焦。 

如果a ≤ f，以上方程不成立，透镜则不能使光束聚焦。 

在射线情况下，傍轴近似满足时透镜方程成立。 

束腰半径 

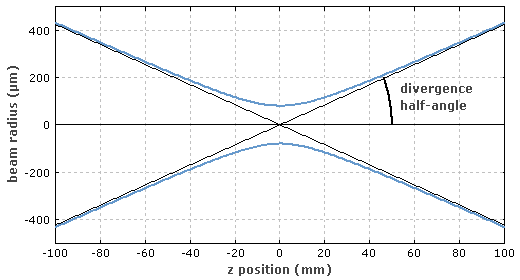
光束半径为 w0的准直高斯光束入射到焦距为f的透镜上，经过透镜后束腰处的半径满足方程： 

1.png

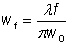
这时假设焦点处光束半径远小于初始光束半径w0。（当光束入射半径很小时该条件不满足，这时焦点比根据上面方程得到的值要大。）同时，还需要假设光束半径远大于波长 λ，这样傍轴近似是满足的。 

根据上面方程发现决定最小光束半径的并不只是焦距f，还有f与透镜孔径半径的比值，这一比值限制了最大光束半径w0。该比值称为透镜的数值孔径。 

这一原理能否用于焦距为f扩展的光学系统取决于采用的焦距的定义。有时需要定义有效焦距来满足这一关系。

光通量(fluence)

定义：单位面积上的光能量。

在基础物理中通量被定义为一些辐射或粒子流的时间积分量。在光学中，光脉冲的光通量F被定义为单位面积上输送的光能。其最常见的单位是J / cm2。 

与光强一样，光通量也是一个与位置相关的数值。对于激光而言，光通量通常在光轴处最大，在远离光轴的地方则会降低。 

在某些情况下，对光通量的最大值更为感兴趣。对于高斯光束，峰值的光通量为总光能量除以π w2 / 2，其中w是高斯光束的光束半径。 

如果知道与时间相关的光强，则可以通过对脉冲的时域积分得到光通量。 

光通量的用途 

当一个强的超短脉冲使得激光晶体或者有源光纤发生增益饱和时，其脉冲脉宽通常远小于上能级寿命。饱和的程度只取决于脉冲光通量，而不是光强的时间分布。增益介质的一个重要特性就是它的饱和通量。 

对于慢的可饱和吸收体，也会发生与增益介质类似的情况。 

在激光脉冲导致激光损伤的情况下，损伤阈值也常被成为光通量。然而损伤阈值并不是一个与脉冲脉宽无关的量，通常情况下，临界的光通量随着脉冲脉宽的上升而上升。

平顶光束(flat-top beams)

定义：光束具有平的强度截面。

平顶光束是指激光光束（通常为经过转换的激光光束）强度截面很大区域内是平的。这与高斯光束不同，高斯光束的强度是从最大值沿着光束轴向外平缓的减小为0. 在有些激光器应用中需要采用这种类型的光束。例如，在处理半导体晶圆或者其它材料时在某些区域需要强度为常数。另外，在高功率时的非线性频率转换过程中，如果采用平顶光束效率会更高。通常，平顶光束边沿比较平滑，因此可近似看做超高斯型，而不是矩形。 

1.png

图1：平顶光束（红色）与高斯光束（绿色）和超高斯强度分布（蓝色）的对比。三束光的功率相同，有效模式面积相等。 

平顶光束的传播 

与高斯光束不同的是，平顶光束不是自由空间的模式。也就是说光束在自由空间中传播时，强度形状会发生变化。强度曲线的边缘越陡，变化越大。图2是模拟的初始为超高斯光束形状的光束的传播情况。 

1.png

图2：初始为超高斯形状的光束在自由空间中传播的演化情况。光束首先被压缩，后来又展开，边缘非常平滑。以上情况下的颜色选取是基于光束轴向饱和时颜色是相同的这一前提。实际上，随着光束的扩展，强度变小。 

实际应用时光束形状的变化可以忽略不计。对于具有更大直径以及边缘变化不剧烈的光束，其大小和形状近似为不变。 

产生平顶光束 

通常需要先从激光器中得到一束高斯光束，然后采用一些合适的光学元件改变其强度形状得到平顶光束。有许多种光束整形器可以改变光束形状。例如，可以采用多个非球面透镜，或者一些衍射光学器件。采用非球面透镜，得到的光束形状非常平坦并且功率效率很高，以及很高的损伤阈值，这在调Q激光器中非常重要。

亮度(Brightness)

定义：通常定性的描述，与激光器的输出功率和光束质量有关；定量化描述需要与照度结合一起。

亮度通常用于激光器和激光光束中，通常是纯描述性的，非定量的应用。而定量的定义不止一个，这就会造成混乱。有时，亮度被看做照度值，而又有些地方被看做辐射量（如下）。重要的差别在于辐照量用于光功率及其相关量，而照度值则是用来估计光辐射的强度。 

尽管美国联邦标准1037C建议将亮度概念在生理感觉方面仅仅作为非定量的参考，但是现在普遍采用它用于其它方面。在激光器技术中，激光光源的亮度（定量情况）通常认为等于其辐射量，是总功率除以焦点模式面积和远场角度的乘积，单位通常为W sr−1 cm−2。本词条下面都采用这一定义。 

具有适中发散角的衍射极限光束（傍轴近似适用），由光束发散角和光束半径之间的关系可得： 

1.png.gif

上式表明，除了与功率和光束质量相关外，亮度还依赖于波长。 

而非衍射极限的光束亮度变小，减小的因子为光束质量因子 M2在x和y方向分量的乘积。 

还有一个定义为光功率除以 M2因子，没有考虑波长。对于衍射极限光束，这一值等于光功率，通常来讲，用其描述在特定孔径和工作距离（有限光束发散角）时焦点处最大光强是非常恰当的。 

亮度是描述激光光束整体的性质，而不是描述某一空间变化的量，例如强度。 

还存在另一个不同的量为光谱亮度。而有些作者有时只提及亮度是非常容易混淆的。另外还有相对亮度，这只是一个定性的量，与照度有关。 

提高亮度 

激光器（光学泵浦）的一个重要特性是产生的激光光束的亮度比泵浦光源的亮度大很多，而输出功率低于泵浦功率，光束质量则比泵浦光源高很多。这种激光器也被称为亮度转换器，尤其是当这一功能在应用中是主要的特点。 

采用低亮度泵浦光源 

在光学泵浦激光器的发展过程中，需要采用低亮度的泵浦光源，因为这一光源在给定输出功率情况下通常比较便宜。例如，大面积激光二极管（也叫做高亮度激光二极管）在单位瓦特的输出功率时的成本比二极管线阵高。然而，低亮度泵浦在激光器设计中也会产生许多不利的效应。并且在不同的条件下产生的效应也不同，在这种情况下，可达到的输出功率、功率效率、脉冲长度或者脉冲重复速率都会比较低。 

这一限制可以与能量转换过程中的熵问题对比理解：熵增加过程可能不会直接造成能量损耗，但是会间接的损耗可用能量。由于光束质量下降而导致亮度减小表示很少模式的光辐射拓展到多个模式中，这确实会提高熵。但是，性能变差并不总是与熵问题直接相关，还部分与增益介质能实现的物理参数以及几何问题相关。

布拉格光栅(Bragg gratings)

定义：包含周期性折射率调制的反射结构。

光学布拉格光栅是具有周期性变化折射率的透明装置，在某一特定波长附近的波长区域（带宽）的反射率很大，该波长满足布拉格条件： 

1.png

其中λ 是真空波长，n是折射率，θ 是在介质中相对于正入射的传播角度， Λ 是光栅周期。如果满足以上条件，光栅的波数与入射和反射波的波数差是匹配的。 

其它波长的光则几乎不受布拉格光栅的影响，不过还是会在反射光谱中产生一些旁瓣。类似的，其它入射角度的光束也几乎不存在反射。 

布拉格波长附近的光束，当光栅足够长时，即使很弱的折射率调制都能实现几乎全反射。由于反射率和折射率与波长有关，布拉格光栅可用做光纤滤波器。 

1.png

图1：布拉格光栅中包含玻璃块用来反射满足布拉格条件的入射光束（左侧）。而其它入射角度的光束则几乎不存在反射。 

光纤布拉格光栅示例 

  • 将布拉格光栅做成体材料（例如，采用玻璃或者聚合物），通常是采用相干紫外光照射光敏玻璃，利用干涉效应进行空间调制，这称为体布拉格光栅（如图1）。它们的反射带宽比介质薄膜反射镜的带宽小很多，因为它们的折射率差较低，可以采用长相互作用长度来进行补偿。（可以实现峰值反射率为99.9%）体布拉格光栅可用于激光二极管中的输出耦合器中；小的反射带宽可以得到窄的辐射带宽（线宽）以及辐射波长对温度的依赖性较低，这在泵浦固态激光器时非常有利。还可以在固态激光器的激光器谐振腔中加入体布拉格光栅，可以稳定或者调谐辐射波长。然而当腔内功率很高时（例如，几十瓦特），存在很多有害的效应，例如反射谱会发生偏移并且反射率减小。当功率不太高时，体布拉格光栅还可以用于频谱组束技术中。 
  • 光纤布拉格光栅是由光纤制作的。它可以反射光纤中的光，或者在多模光纤中得到各种类型的模式耦合。光纤布拉格光栅用于光纤激光器中可以固定波长，或者滤除掉特定波长成分，或者用在光纤放大器中实现增益平坦以及光纤传感器中。 
  • 有些激光二极管包含内置布拉格光栅（采用半导体技术制作）用来窄化和稳定辐射波长（参阅分布布拉格反射激光器，分布反馈激光器）。
双折射(birefringence)

定义：双折射现象或者介质折射率与偏振有关。

文献中，双折射通常包含两种不同的含义。经典光学中，就是下面所说的双折射（double refraction）。而在非线性光学和激光器技术中，双折射则是一些非各向同性透明介质的折射率依赖于偏振方向（即电场方向）的性质。后者的性质时非偏振光束入射到该材料上时产生双折射。 

折射率依赖于偏振态的结果 

折射率依赖于偏振态会产生下面的一些效应： 

  • 当光束在双折射晶体表面发生折射是，折射角与偏振方向有关。这样非偏振光束在非垂直入射到材料中的情况下分为两个线性偏振的光（双折射）。当非偏振光射向一个物体，如果采用双折射晶体看该物体，会出现两个像。 
  • 当线偏振激光光束在双折射晶体中传输时，如果偏振方向与双折射轴不重合，这时会包含两个方向具有不同波数的偏振部分。因此，在传输过程中，由于两偏振分量之间存在相对相位变化，于是偏振状态发生变化。这一效应可应用于双折射调谐器中，因为它是与波长相关的（尽管折射率差与波长无关）。该效应通过自相位调制和交叉相位调制而与功率相关（参阅非线性偏振态旋转），有时用于光纤激光器中的被动锁模。 
  • 类似的，激光光束在存在热效应诱导的双折射效应的激光器晶体中传输时，偏振态也发生变化。这一变化与位置有关，因为双折射轴方向是变化的（例如，通常是轴向变化）。这一变化（与激光器谐振腔中的偏振光元件结合）是去极化损耗的来源。 
  • 非线性晶体材料的双折射可以实现非线性作用时的双折射相位匹配。 

双折射举例 

在激光器技术和非线性光学中，双折射现象通常发生在非各向同性晶体中： 

  • 一些激光器晶体（例如，钒酸盐晶体和钨酸盐晶体）本身就具有双折射。这在需要无去极化损耗的线偏振输出时非常有用。 
  • 所有用于非线性频率转换的非线性晶体都存在双折射。 
  • 双折射晶体通常用来制作偏振器。 
  • 尽管光纤本身不具有双折射，光纤光学中常常遇到双折射效应：有时双折射来自于光纤弯曲（引起弯曲损耗）和随机扰动。并且还存在保偏光纤。 

即使是各向同性介质，也会由于存在不均匀的机械应力而产生双折射。这可以在两个交叉偏振器间放置一块有机玻璃观察：当施加应力到有机玻璃上，可以看到由于应力诱导的与波长相关的双折射效应而产生的彩色图像。弯曲光纤中也存在类似的效应，由于激光器晶体中的热效应，会产生去极化损耗。 

直光纤只有很小的随机双折射，即使这样其中的光传输一段距离后偏振状态也会发生变化。存在保偏光纤，是利用了很强的双折射来抑制这些效应。 

定量描述双折射 

可以采用下列方法定量描述双折射的大小： 

  • 对于晶体，可以考虑量偏振方向的折射率差值。 
  • 光纤和其它波导中，采用有效折射率差值描述更好。这与传播常数虚部的差值直接相关。 
  • 还可以用偏振拍长来表征，是2π 除以传播常数的差值。如果波导中同时存在不同偏振状态的波，经过整数倍的偏振拍长，它们的相位关系不变的。
光束参量乘积(beam parameter product)

定义：缩写：BPP 焦点处光束半径和远场发散角的乘积。

激光光束的光束参量乘积（BPP）是光束半径（束腰处）与半发散角（远场）的乘积。常用单位为 mm mrad（毫米乘以毫弧度）。BPP通常用来表征激光光束的光束质量：光束参量乘积越大，光束质量越差。 

若定义非高斯光束的BPP需要重新定义光束半径和发散角。衍射极限高斯光束能达到的最小光束参量乘积为λ / π。例如，1064 nm光束的最小光束参量乘积约为0.339 mm mrad。 

1.png

图1：不同类型激光器的光束参数乘积与M2值。由于激光器波长更长，其光束参量乘积比衍射极限的固态激光器大，但是比灯泵浦系统小。 

非圆形截面光束在垂直方向与水平方向的BPP值是不同的。 

光束在无象差光学系统中传输时，例如薄透镜，BPP值不变。如果该透镜使光束会聚，半径小于束腰半径，那么光束发散角相应的会增大。为了测量BPP，需要将光束会聚成某一合适尺寸，该尺寸取决于采用的仪器装置（例如，光束分析仪）和空间大小（需要几个瑞利长度）。 

非理想的光学装置会损坏光束质量，使BPP值增大。有些特殊情况下，光学元件的很小象差（例如球形棱镜）还会减小光束的BPP值，这时光束畸变会被该元件补偿。 

一个常用的相关的量为直径发散角乘积。 

光束发散角(beam divergence)

定义：衡量光束从其中心向外发散的程度。

激光光束的光束发散角是用来衡量光束从束腰向外发散的速度。在激光笔或者自由空间光通信的应用中需要非常低的光束发散角。具有非常小发散角的光束，例如光束半径在很长的传输距离内接近常数，被称为准直光束。 

1.png

图1：高斯光束的半发散角是根据光束半径（蓝线）的在传输方向上的渐变得到的。然而，本图中的发散角比实际上大很多，x和y轴的标度和实际中也是不一样的。 

由于波动性，光束中存在一些发散是不可避免的（假设光在各向同性介质中传输）。紧聚焦光束的发散角更大。如果一个光束发散角远大于物理上决定的发散角，那么光束就具有很差的光束质量。下面定量表示发散角后会给出更多细节讨论。 

目录

  1. 光束发散角的定量表示
  2. 高斯光束的发散角和质量较差的光束
  3. 空间傅里叶变换
  4. 测量光束发散角

光束发散角的定量表示 

存在很多关于发散角的定量定义： — 最常用的定义是，光束发散角为光束半径对远场轴向位置的导数，也就是与束腰的距离远大于瑞利长度。这一定义延伸出半发散角概念（单位为弧度），依赖于光束半径的定义。对于高斯光束，光束半径通常定义为处于峰值强度的 1/e2 处对应的半径。而非高斯形状的光束，可以采用积分公式，在光束半径词条中有具体讨论。有时采用全角度，是半发散角的两倍。 — 除了在高斯光束中取处于 1/e2 峰值强度处对应的点的角度作为发散角之外，还可以采用半高全宽（FWHM）发散角。在激光二极管和发光二极管数据表格中通常采用。高斯光束中，采用这种定义的发散角是由高斯光束半径确定的半发散角的1.18倍。 

举个例子，小的边发射激光二极管快轴对应的FWHM光束发散角为30°。这对应 25.4° = 0.44 rad 1/e2的半发射角，很显然为了在不截断它的情况下使这一光束准直需要采用相当大数值孔径的棱镜。很大发散的光束需要采用一些光学装置以避免球面象差引起的光束质量下降。 

高斯光束的发散角和质量较差的光束 

对于衍射极限的高斯光束，1/e2 光束半发散角为λ / (π w0)，其中 λ 是波长，w0是束腰半径。这一方程基于傍轴近似，因此只有当光束发散角不是很大时才适用。 

给定光束半径，更大的光束发散角，也就是，更大的光束参数乘积，与光束质量有关，代表将光束会聚成非常小的点的可能性更小。如果用因子 M2来表征光束质量，那么半发散角为： 

1.png

举个例子，Nd:YAG激光器产生的1064 nm的光束具有理想的光束质量（M2 = 1），光束半径为1 mm，半发散角只有 0.34 mrad = 0.019°。 

空间傅里叶变换 

将激光光束的复电场空间进行傅里叶变换变为横向坐标的函数是非常实用的（傅里叶光学）。这样可把光束看做一系列平面波的叠加，而傅里叶变换表明平面波的振幅和相位都进行变换。在自由空间中传播时，只有相位值有变化。 

空间傅里叶变换的宽度，例如均方根宽度，与光束发散角有直接关系。这表示通过计算光束轴向任一点的横向复振幅就可以得到光束发散角，这里假设光束是在各向同性介质中传播（例如空气）。 

测量光束发散角 

为了测量光束发散角，通常测量光束散焦度，也就是采用光束分析仪测量不同位置的光束半径。 

也可以从某一平面的复振幅分布来得到光束发散角。这些数据可利用Shack-Hartmann波前传感器来得到。