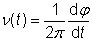Tag 玻璃透镜

光子(photons)

定义：光能量的量子。

相关词条：非经典光受激辐射光子计数声子自发辐射

当一束很弱的光束进入一个很灵敏的光电探测器，可以发现能量是以小束的形式传播的，而不是连续的。这可以解释成光束包含了一束束的能量，称为量子或者光量子。光子能量为h ν = h c / λ，即普朗克常数h与光频率ν的乘积。在二十世纪，Max Planch处理热辐射问题中就采用了光包含能量束的观点，Albert Einstein在研究光电效应时也利用了这一观点。光子则是在1926年物理化学家 Gilbert N. Lewis定义的。 

将光子看做光的粒子可以帮助理解许多量子现象，但是如果不了解其限制因素则很容易得出错误的结论。现代量子光学给出了非常自洽的、但是不是很简洁的对光的本性的描述。这里将光子看做量子化电磁场的元激发。这一理论框架下光子的性质比较特别，不能采用简单的粒子图像或者纯波动图像来解释。 

光子的一些关键性质 

1. 光的传播（在自由空间或者波导中）实际就是波的传播。某时刻某一点的量子力学场振幅是光所有可能路径的叠加。叠加可能会干涉相长或者相消，这是光学干涉效应的基础。纯粒子图像很难与实验观察相符，例如，在传统的双缝干涉实验中，每一个粒子都会通过其中一条缝，而与另一条缝不相干；但是这无法解释只有当堵住一条缝之后，有些粒子才能到达某一位置，而两条缝都打开时就不能到达该位置的现象（相消干涉）。 
2. 当光与原子或者其它粒子发生相互作用时，只有是光子能量h ν整数倍的能量才能够被光场吸收或者释放。这可以简单的理解为只能吸收或辐射一定数目的光子。只有当作用的粒子（例如原子）能够接收这些能量时，相互作用过程才会发生，即它们量子力学能级间的能级差对应光子能量，或者是光子能量整数倍（参阅双光子吸收）。纯的波动图像将这些能量限制看做共振效应，但是无法解释能量的量子化现象。 
3. 在灵敏的光电探测器中，能量量子化特别明显，可以进行光子计数，即能够探测单光子吸收效应。这在很多的科学和技术领域都有应用。 
4. 光子的静止质量为0，因此不能使其变慢或者静止。存在所谓的慢光现象，是由于电磁场与物质之间强烈的相互作用引起的，因此只有在介质中才存在这种现象。这时并不仅仅是电磁场激发，纯的光子图像不能给出很合理的解释。 
5. 由于光子的泊松特性，多个光子倾向于激发相同模式的辐射场。例如，受激辐射过程中（激光器中很重要）就能发现，还可以在热激发辐射后的能量谱中看到（黑体辐射）。 
6. 光子可以以纠缠态存在，即不同光子的有些性质（例如，偏振）0是相干的，尽管只有当进行测量时这些性质才具有特定的值。由于对不同光子的测量可以发生在不同的位置，这似乎意味着超光速传输信息是可能的（Einstein-Podolsky-Rosen佯谬），但是实际上是不会发生的。 

量子理论不仅能应用到可见光中，它还可以应用到任意的电磁波现象中。但是在射频技术中，量子效应并不像在光学和激光器技术中这么重要。这是因为射电波的光子能量与其室温下的热能相比很小，而光学现象中则刚好相反。 

在激光物理中，常见的现象是光子在介质中传播，例如，透明晶体或者玻璃，以及激光增益介质。这时严格来说称为光子就不合适了，因为电磁波会与介质发生相互作用，因此传播的是准粒子，有时称为极化激元，类似于电磁场的激发态与极化介质耦合的产物。 

定义：将功率或者能量分解成不同波长或者频率。

相关词条：功率谱密度光谱仪光梳带宽

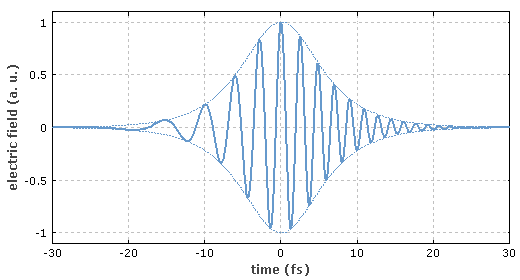
光源或者一些光束的光谱（或辐射谱）或者包含了能量和功率在不同波长中分布的信息。通常它是用图表的形式表示，给出了功率谱密度随波长或者光功率之间的关系曲线。图1就是一个例子，给出了超连续光源的数值模拟光谱。单频激光器的光谱不同于图中的宽谱，是由非常窄的线表征，极限情况下线宽仅为1Hz量级，对应的波长范围只有约≈ 3 •10−12 nm（中心波长为1微米）。其它的激光器包含多条线，有的具有很大的带宽（尤其是超短脉冲的锁模激光器），约为100 nm，具有频率梳结构。 

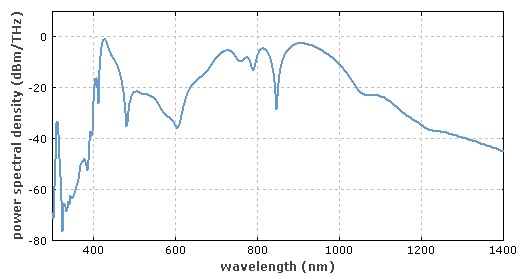
图1：数值模拟超连续光源。参阅词条超连续产生得到更多细节。 

可以采用不同类型的光谱仪来接收光谱，它们适用的光谱范围及光谱分辨率都是不同的。 

光谱与光的时间相干特性密切相关。例如，由时间相干方程可以得到光谱。光谱还与电场的傅里叶变化有关，但是后者大多数情况下不能直接得到。因此，也称为光场的傅里叶光谱。 

光学带宽 

光学带宽就是指光谱的宽度。具有不同的定义，常用的是半高全宽（FWHM）。 

具有线结构的光谱 

有些光源的光谱非常平坦，例如白炽灯，光二极管或者超发光光源。而有些光源的谱中包含相距很近的窄线，只能从具有足够高光谱分辨率（小的分辨率带宽）的光谱仪中能够看到。例如，连续光激光器辐射多模光束，并且只辐射基本谐振腔模式时，光谱中的线是几乎是等间距的，并且间距等于谐振腔往返时间的倒数，在MHz或者GHz范围。如果激光器同时辐射高阶横模，那么光谱中存在附加的线，这时光谱会更加紧密并且是不等间距的。但是任意的锁模激光器都会产生等间距的频率梳光谱，同时光谱中还存在较弱的激光器噪声。 

定义：单位面积的光功率。

相关词条：强度噪声亮度高斯光束激光光束激光诱导损伤

激光光束的光强I，是单位面积的光功率，这时假设光束穿过一个与传播方向垂直的假想的平面。光强的单位为W/m2或W/cm2。光强是光子能量与光通量的乘积。 

对于单色光波，例如平面波或者高斯光束，强度与电场振幅之间的关系为： 

其中vp为相速度，c为真空光速，n是折射率。在不考虑拍音的情况下，非单色光波的强度分布是不同空间成分的简单相加。 

以上方程并不是对于任意电磁场都成立。例如，衰逝场具有有限的电场振幅但是不能传输任何能量。因此需要将光强定义为坡印廷矢量的幅值。 

如果激光光束的强度截面为平顶形状（即在某一区域强度为常数，其它地方强度为0），那么强度就是总功率除以光束面积。对于高斯光束，如果功率为P，光束半径为w，那么峰值强度为： 

是常采用的值的两倍。将该方程对整个光束面积积分就得到总功率。 

激光器中的高阶横向谐振腔模式被激发后，得到多模激光光束，由于各模式间的相对相位是随时间变化的，因此强度的横截面也会发生变化。这时峰值强度可能位于离光束轴一段距离的位置。 

强度通常用到一些非定量的不精确的地方，与光功率没有严格的区分。例如，强度噪声通常是指光功率的噪声（涨落）。 

在下列情况下需要考虑光强： 

• 在激光器增益介质中，光强与跃迁截面决定了光跃迁的速率。当强度大于饱和强度时，稳态的光跃迁过程会发生饱和效应。 
• 透明介质的克尔效应引起的折射率变化等于非线性系数乘以光强度。 
• 当强度大于损伤阈值时，会发生介质的光学损伤，一般只由光脉冲产生，并且与脉冲长度有关。 
• 放大的超短脉冲可以达到非常高的峰值强度。当气体中的强度为甚至更高时，会产生高次谐波。 

光束质量分析仪可以用来测量激光光束强度截面的形状。 

定义：激光光束与谐振腔或者波导模式的电场分布是完全的空间匹配。

相关词条：模式腔衍射极限光束激光光束

在很多情况下，需要将激光光束与另一光束或模式严格匹配从而可以得到有效的耦合。例如： 

• 激光器产生的光束需要耦合进光纤中。 
• 激光光束需要与无源光学谐振腔匹配，作为空间或者光谱滤波器（参阅模清洁腔）。 
• 注入锁定时，主激光器的模式需要与从属激光器的模式匹配。 

模式的匹配不仅要求强度截面在空间上是交叠的，还需要相位截面也是匹配的。如果两光束的复振幅在某一平面上完全匹配，那么在传播过程中会始终保持匹配的。可以采用合适的替续光学系统实现模式匹配（通常是一些曲面镜或透镜的组合），但是前提是初始光束的光束质量接近于衍射极限。 

数学上，模式匹配量可以由以下交叠积分定量表示： 

其中 E1和E2 是平面上的复电场，代表一束激光光束和谐振腔或者波导模式的场，积分区域为整个光束截面。该积分比值在自由空间中传播时保持不变。 

以上的交叠积分在计算模式振幅时非常重要。在许多情况下，例如将光功率耦合进某一模式时，需要计算以上交叠积分的平方。 

如果光束来自于频率可调谐的单频激光器，射向对称的法布里-珀罗干涉仪，如果把激光频率在谐振腔的整个自由光谱范围内调谐，那么可以利用得到的透射光分析模式匹配的程度。当与腔模式完全匹配时（通常是基模，即高斯模式），并且满足共振条件时，就能得到谐振腔完全的透射，此时不会激发其它共振模式。

定义：振荡相位随时间的微分除以2π。

相关词条：频率噪声线宽啁啾光谱图

在描述非单色信号时需要用到瞬时频率，它的定义式为： 

也就是振荡相位 φ对时间的微分。（除去因子 1/2π，就得到瞬时角频率。）与傅里叶频率不同的是，瞬时频率通常与时间有关。正弦信号的瞬时频率是常数等于振荡的频率。 

图1：强上啁啾脉冲的电场，其中瞬时频率随时间增加而增大。 

在考虑频率噪声和相位噪声时，瞬时频率非常重要，它也经常用于啁啾光脉冲（图1），其瞬时频率与时间有关。基本思想比傅里叶频率要更加直观。在音乐中也有相同的概念：乐谱中将音符表示为时间间隔，每一个间隔内的瞬时频率为一个定值（对应于音调）。然而，这一概念对于复杂的信号，例如白噪声，就出现问题了。在激光器中，很容易对单频激光器定义瞬时频率，而对于多模激光器，则首先需要将各个不同频率组分分离开（采用滤波技术），然后才能得到瞬时频率。在啁啾光脉冲中瞬时频率概念也是很有用处的，其中不同脉冲的瞬时频率是不同的。 

振荡信号的傅里叶光谱并不代表瞬时频率的概率分布，因此采用这一光谱测量的线宽也不是瞬时频率的均方根值。瞬时频率域傅里叶频率之间的关系更加复杂和微秒。 

瞬时频率随时间的变化可以根据光谱图的出来。但是，仅仅一个瞬时频率随时间变化的曲线并不能给出全部变化信息。 

测量瞬时频率 

电子信号（例如，拍音）的瞬时频率可以由锁相环路（PLL）得出，环路包含一个电压控制振荡器（VCO）和反馈系统的鉴相器使VCO与入射信号同步。VCO的入射信号可以测量瞬时频率。 这一方案的原理也可以运用到相位跟踪器软件中，来测量记录信号的瞬时频率。这一方案很简单但是也有一些缺点，尤其是其有限的带宽，存在延迟响应。快速傅里叶变换方法更加强大，但是也会更加复杂。

定义：插入某一器件产生的功率损耗。

义：波长在750nm和1mm之间的不可见光。

相关词条：紫外光二氧化碳激光器中红外激光光源量子级联激光器

红外光的波长大于700-800nm，即可见光的波长上限。二者的界限并不是很明确，在该区域眼睛的响应度非常缓慢的减小。尽管在700nm时响应度已经很低，但是当激光二极管的光足够强，波长为750nm时也是可以看到的。尽管这些光并不亮，但是对眼睛是有伤害的。红外光谱的上限也是没有明确的定义的，通常认为约等于1mm。 

不同的红外光谱区域的定义为： 

• 近红外区域（也称为IR-A），波长从约700 nm到1400 nm。在这一波长区域工作的激光器对眼睛伤害很大，因为近红外光同可见光一样可以穿透并且聚焦于视网膜，但是不会引起起保护作用的眨眼反射。因此需要进行眼睛防护。 
• 中红外光（MWIR）波长从3到8微米。大气对该波段的光有强烈的吸收，具有许多吸收线，例如二氧化碳（CO2）和水蒸气（H2O）。许多气体具有很强的中红外吸收线，因此这一光谱区域的光可用于气体光谱学。 
• 长波红外光（LWIR）波长从8到15微米，后面为远红外（FIR），波长范围到1 mm，有时认为从8微米开始。这一光谱区域可用于热成像。 

一定要注意的是，实际中这些区域的定义有些变化。 

许多玻璃对于近红外光是透明的，但是在更长波长时吸收很强，因为这时光子可以直接转化为声子。对于二氧化硅玻璃，强吸收发生在波长约为2微米时。 

红外光也称为热辐射，因为热体的热辐射通常在红外波长范围内。即使在室温或者低于室温时，热体也会辐射很强的中红外和远红外光，可以用于热成像。例如，冬季供暖房子的红外成像可以显示屋内存在热泄漏（例如，在窗户、屋顶等），因此可以提高直接探测的效率。 

红外辐射源 

大多数激光器，例如Nd:YAG 激光器，光纤激光器以及高功率激光二极管都会辐射近红外光。而产生中红外和远红外光谱的激光器则相对较少。二氧化碳激光器辐射的光为1060 nm和该区域内其它波长的光。固体中红外激光器的激光晶体存在的普遍问题是宿主介质有限的透明度，以及存在快速多光子跃迁过程取代激光跃迁过程；需要声子能量很低的晶体材料。低温铅盐激光器是早期经常采用的中红外光谱学光源，但是现在被量子级联激光器取代，该激光器甚至在室温时都能实现连续波工作。自由电子激光器可以用做宽带调谐的红外光光源。 

红外光也可由非线性频率转换过程产生。例如，中红外光可由非线性晶体材料的差频产生得到，或者由光学参量振荡器得到。可以参阅词条中红外激光器光源。 

普通的电灯泡辐射的红外光比可见光多，因此其功率转化效率只有5-10%。太阳光也包含很强的红外成分。 

红外光探测 

可以采用很多类型的光电探测器探测红外光。例如，采用半导体的光电二极管带隙能量足够小，这样载流子不仅能被光激光还能被热能量激发，因为在室温下光子能量比kBT大不了很多。因此，红外探测器需要冷却到足够低的温度来提高其灵敏度。红外相机也需要如此。 

尤其是近红外光，存在红外线探测器，一些风景中辐射的红外线在红外敏感的光阴极上成像，并且显示出来，例如绿色。这些红外线探测器通常用于激光器实验室中用来追踪红外激光光束。

定义：真空中光速与介质中群速度的比值。 符号：ng

相关词条：群速度折射率

与折射率的定义类似，群速度折射率（或群速度系数）被定义为真空中光速与介质中群速度的比值： 

群速度折射率常用于计算超短脉冲在介质中传播时的时延，也用于计算含有色散介质的谐振腔的自由光谱范围。 

对于晶体或者玻璃，在可见光或近红外光谱范围内的群速度折射率通常要大于普通的折射率（与相速度相关）。 

图 1：0℃（蓝色），100℃（黑）和200℃（红色）下的石英的折射率曲线（实线）和群速度折射率曲线（虚线）。