Tag LED模组

定义：将功率或者能量分解成不同波长或者频率。

相关词条：功率谱密度光谱仪光梳带宽

光源或者一些光束的光谱（或辐射谱）或者包含了能量和功率在不同波长中分布的信息。通常它是用图表的形式表示，给出了功率谱密度随波长或者光功率之间的关系曲线。图1就是一个例子，给出了超连续光源的数值模拟光谱。单频激光器的光谱不同于图中的宽谱，是由非常窄的线表征，极限情况下线宽仅为1Hz量级，对应的波长范围只有约≈ 3 •10−12 nm（中心波长为1微米）。其它的激光器包含多条线，有的具有很大的带宽（尤其是超短脉冲的锁模激光器），约为100 nm，具有频率梳结构。 

图1：数值模拟超连续光源。参阅词条超连续产生得到更多细节。 

可以采用不同类型的光谱仪来接收光谱，它们适用的光谱范围及光谱分辨率都是不同的。 

光谱与光的时间相干特性密切相关。例如，由时间相干方程可以得到光谱。光谱还与电场的傅里叶变化有关，但是后者大多数情况下不能直接得到。因此，也称为光场的傅里叶光谱。 

光学带宽 

光学带宽就是指光谱的宽度。具有不同的定义，常用的是半高全宽（FWHM）。 

具有线结构的光谱 

有些光源的光谱非常平坦，例如白炽灯，光二极管或者超发光光源。而有些光源的谱中包含相距很近的窄线，只能从具有足够高光谱分辨率（小的分辨率带宽）的光谱仪中能够看到。例如，连续光激光器辐射多模光束，并且只辐射基本谐振腔模式时，光谱中的线是几乎是等间距的，并且间距等于谐振腔往返时间的倒数，在MHz或者GHz范围。如果激光器同时辐射高阶横模，那么光谱中存在附加的线，这时光谱会更加紧密并且是不等间距的。但是任意的锁模激光器都会产生等间距的频率梳光谱，同时光谱中还存在较弱的激光器噪声。 

定义：单位面积的光功率。

相关词条：强度噪声亮度高斯光束激光光束激光诱导损伤

激光光束的光强I，是单位面积的光功率，这时假设光束穿过一个与传播方向垂直的假想的平面。光强的单位为W/m2或W/cm2。光强是光子能量与光通量的乘积。 

对于单色光波，例如平面波或者高斯光束，强度与电场振幅之间的关系为： 

其中vp为相速度，c为真空光速，n是折射率。在不考虑拍音的情况下，非单色光波的强度分布是不同空间成分的简单相加。 

以上方程并不是对于任意电磁场都成立。例如，衰逝场具有有限的电场振幅但是不能传输任何能量。因此需要将光强定义为坡印廷矢量的幅值。 

如果激光光束的强度截面为平顶形状（即在某一区域强度为常数，其它地方强度为0），那么强度就是总功率除以光束面积。对于高斯光束，如果功率为P，光束半径为w，那么峰值强度为： 

是常采用的值的两倍。将该方程对整个光束面积积分就得到总功率。 

激光器中的高阶横向谐振腔模式被激发后，得到多模激光光束，由于各模式间的相对相位是随时间变化的，因此强度的横截面也会发生变化。这时峰值强度可能位于离光束轴一段距离的位置。 

强度通常用到一些非定量的不精确的地方，与光功率没有严格的区分。例如，强度噪声通常是指光功率的噪声（涨落）。 

在下列情况下需要考虑光强： 

• 在激光器增益介质中，光强与跃迁截面决定了光跃迁的速率。当强度大于饱和强度时，稳态的光跃迁过程会发生饱和效应。 
• 透明介质的克尔效应引起的折射率变化等于非线性系数乘以光强度。 
• 当强度大于损伤阈值时，会发生介质的光学损伤，一般只由光脉冲产生，并且与脉冲长度有关。 
• 放大的超短脉冲可以达到非常高的峰值强度。当气体中的强度为甚至更高时，会产生高次谐波。 

光束质量分析仪可以用来测量激光光束强度截面的形状。 

定义：激光光束与谐振腔或者波导模式的电场分布是完全的空间匹配。

相关词条：模式腔衍射极限光束激光光束

在很多情况下，需要将激光光束与另一光束或模式严格匹配从而可以得到有效的耦合。例如： 

• 激光器产生的光束需要耦合进光纤中。 
• 激光光束需要与无源光学谐振腔匹配，作为空间或者光谱滤波器（参阅模清洁腔）。 
• 注入锁定时，主激光器的模式需要与从属激光器的模式匹配。 

模式的匹配不仅要求强度截面在空间上是交叠的，还需要相位截面也是匹配的。如果两光束的复振幅在某一平面上完全匹配，那么在传播过程中会始终保持匹配的。可以采用合适的替续光学系统实现模式匹配（通常是一些曲面镜或透镜的组合），但是前提是初始光束的光束质量接近于衍射极限。 

数学上，模式匹配量可以由以下交叠积分定量表示： 

其中 E1和E2 是平面上的复电场，代表一束激光光束和谐振腔或者波导模式的场，积分区域为整个光束截面。该积分比值在自由空间中传播时保持不变。 

以上的交叠积分在计算模式振幅时非常重要。在许多情况下，例如将光功率耦合进某一模式时，需要计算以上交叠积分的平方。 

如果光束来自于频率可调谐的单频激光器，射向对称的法布里-珀罗干涉仪，如果把激光频率在谐振腔的整个自由光谱范围内调谐，那么可以利用得到的透射光分析模式匹配的程度。当与腔模式完全匹配时（通常是基模，即高斯模式），并且满足共振条件时，就能得到谐振腔完全的透射，此时不会激发其它共振模式。

定义：振荡相位随时间的微分除以2π。

相关词条：频率噪声线宽啁啾光谱图

在描述非单色信号时需要用到瞬时频率，它的定义式为： 

也就是振荡相位 φ对时间的微分。（除去因子 1/2π，就得到瞬时角频率。）与傅里叶频率不同的是，瞬时频率通常与时间有关。正弦信号的瞬时频率是常数等于振荡的频率。 

图1：强上啁啾脉冲的电场，其中瞬时频率随时间增加而增大。 

在考虑频率噪声和相位噪声时，瞬时频率非常重要，它也经常用于啁啾光脉冲（图1），其瞬时频率与时间有关。基本思想比傅里叶频率要更加直观。在音乐中也有相同的概念：乐谱中将音符表示为时间间隔，每一个间隔内的瞬时频率为一个定值（对应于音调）。然而，这一概念对于复杂的信号，例如白噪声，就出现问题了。在激光器中，很容易对单频激光器定义瞬时频率，而对于多模激光器，则首先需要将各个不同频率组分分离开（采用滤波技术），然后才能得到瞬时频率。在啁啾光脉冲中瞬时频率概念也是很有用处的，其中不同脉冲的瞬时频率是不同的。 

振荡信号的傅里叶光谱并不代表瞬时频率的概率分布，因此采用这一光谱测量的线宽也不是瞬时频率的均方根值。瞬时频率域傅里叶频率之间的关系更加复杂和微秒。 

瞬时频率随时间的变化可以根据光谱图的出来。但是，仅仅一个瞬时频率随时间变化的曲线并不能给出全部变化信息。 

测量瞬时频率 

电子信号（例如，拍音）的瞬时频率可以由锁相环路（PLL）得出，环路包含一个电压控制振荡器（VCO）和反馈系统的鉴相器使VCO与入射信号同步。VCO的入射信号可以测量瞬时频率。 这一方案的原理也可以运用到相位跟踪器软件中，来测量记录信号的瞬时频率。这一方案很简单但是也有一些缺点，尤其是其有限的带宽，存在延迟响应。快速傅里叶变换方法更加强大，但是也会更加复杂。

定义：插入某一器件产生的功率损耗。

义：波长在750nm和1mm之间的不可见光。

相关词条：紫外光二氧化碳激光器中红外激光光源量子级联激光器

红外光的波长大于700-800nm，即可见光的波长上限。二者的界限并不是很明确，在该区域眼睛的响应度非常缓慢的减小。尽管在700nm时响应度已经很低，但是当激光二极管的光足够强，波长为750nm时也是可以看到的。尽管这些光并不亮，但是对眼睛是有伤害的。红外光谱的上限也是没有明确的定义的，通常认为约等于1mm。 

不同的红外光谱区域的定义为： 

• 近红外区域（也称为IR-A），波长从约700 nm到1400 nm。在这一波长区域工作的激光器对眼睛伤害很大，因为近红外光同可见光一样可以穿透并且聚焦于视网膜，但是不会引起起保护作用的眨眼反射。因此需要进行眼睛防护。 
• 中红外光（MWIR）波长从3到8微米。大气对该波段的光有强烈的吸收，具有许多吸收线，例如二氧化碳（CO2）和水蒸气（H2O）。许多气体具有很强的中红外吸收线，因此这一光谱区域的光可用于气体光谱学。 
• 长波红外光（LWIR）波长从8到15微米，后面为远红外（FIR），波长范围到1 mm，有时认为从8微米开始。这一光谱区域可用于热成像。 

一定要注意的是，实际中这些区域的定义有些变化。 

许多玻璃对于近红外光是透明的，但是在更长波长时吸收很强，因为这时光子可以直接转化为声子。对于二氧化硅玻璃，强吸收发生在波长约为2微米时。 

红外光也称为热辐射，因为热体的热辐射通常在红外波长范围内。即使在室温或者低于室温时，热体也会辐射很强的中红外和远红外光，可以用于热成像。例如，冬季供暖房子的红外成像可以显示屋内存在热泄漏（例如，在窗户、屋顶等），因此可以提高直接探测的效率。 

红外辐射源 

大多数激光器，例如Nd:YAG 激光器，光纤激光器以及高功率激光二极管都会辐射近红外光。而产生中红外和远红外光谱的激光器则相对较少。二氧化碳激光器辐射的光为1060 nm和该区域内其它波长的光。固体中红外激光器的激光晶体存在的普遍问题是宿主介质有限的透明度，以及存在快速多光子跃迁过程取代激光跃迁过程；需要声子能量很低的晶体材料。低温铅盐激光器是早期经常采用的中红外光谱学光源，但是现在被量子级联激光器取代，该激光器甚至在室温时都能实现连续波工作。自由电子激光器可以用做宽带调谐的红外光光源。 

红外光也可由非线性频率转换过程产生。例如，中红外光可由非线性晶体材料的差频产生得到，或者由光学参量振荡器得到。可以参阅词条中红外激光器光源。 

普通的电灯泡辐射的红外光比可见光多，因此其功率转化效率只有5-10%。太阳光也包含很强的红外成分。 

红外光探测 

可以采用很多类型的光电探测器探测红外光。例如，采用半导体的光电二极管带隙能量足够小，这样载流子不仅能被光激光还能被热能量激发，因为在室温下光子能量比kBT大不了很多。因此，红外探测器需要冷却到足够低的温度来提高其灵敏度。红外相机也需要如此。 

尤其是近红外光，存在红外线探测器，一些风景中辐射的红外线在红外敏感的光阴极上成像，并且显示出来，例如绿色。这些红外线探测器通常用于激光器实验室中用来追踪红外激光光束。

定义：真空中光速与介质中群速度的比值。 符号：ng

相关词条：群速度折射率

与折射率的定义类似，群速度折射率（或群速度系数）被定义为真空中光速与介质中群速度的比值： 

群速度折射率常用于计算超短脉冲在介质中传播时的时延，也用于计算含有色散介质的谐振腔的自由光谱范围。 

对于晶体或者玻璃，在可见光或近红外光谱范围内的群速度折射率通常要大于普通的折射率（与相速度相关）。 

图 1：0℃（蓝色），100℃（黑）和200℃（红色）下的石英的折射率曲线（实线）和群速度折射率曲线（虚线）。

定义：窄带光脉冲在光学器件中的时间延迟。

相关词条：群时延色散群速度超光速传输偏振模式色散频谱相位

光学元件（例如，介质反射镜或者光纤）的群时延（Tg）的定义为光谱相位对角频率的微分： 

其单位与时间相同，并且与频率（参阅群延时色散，色散）、偏振态（偏振模式色散）和光模式（模间色散）有关。 

具有简单时间和空间形状的窄带光脉冲在线性传播时，群时延就是指脉冲峰值穿过光学元件后的时间延迟。而对于宽带光脉冲来说，尤其是在传播过程中受到非线性效应的影响情况下，情况非常复杂。如果对群时延的描述不恰当则会得出错误的结果。 

在普通的固体介质中，例如激光晶体或者光纤，群时延与长度和相速度比值相差比较多。例如，一米的熔融二氧化硅体材料对1550nm的光产生的群时延为4.879 ns，而由相速度得到的结果为4.817 ns。而更短波长时，例如400 nm时，差值更大：群时延为5.049 ns。光纤中的群时延还受纤芯中掺杂的物质和波导色散效应的影响。 

光学谐振腔中往返一周的群时延决定了共振腔模式之间的间隔，即自由光谱范围。 

可以采用很多方法测量光学元件的群时延。最直接的方法是测量超短脉冲到达的时间。还存在更加强大的干涉方法，例如，采用白光干涉仪，测量的精度在几个飞秒。 

介质中光波的群速度等于单位长度群时延的倒数。 

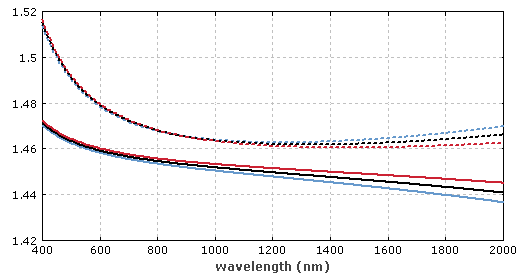
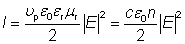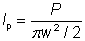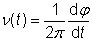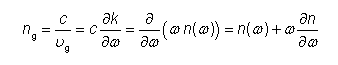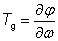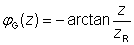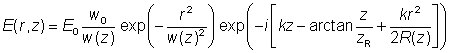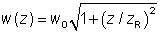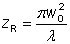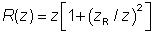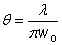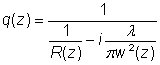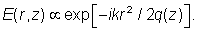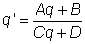定义：光束在垂直于光轴平面上的电场可由高斯方程表示，有时还会有附加的抛物线型相位曲线。

相关词条：模式ABCD矩阵光束参量乘积光束质量光束半径束腰准直光束衍射极限光束古依相移激光光束M2因子

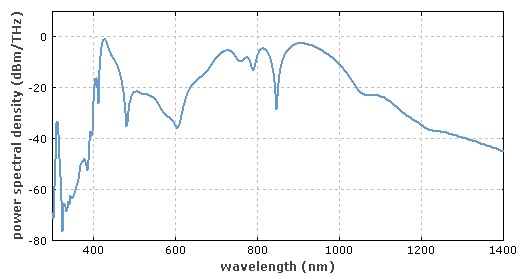
尤其是在激光物理中，激光光束通常为高斯光束，是以数学家和物理学家Johann Carl Friedrich Gauß命名。这时功率为P的光束光强的横断面可由高斯方程表示： 

这里光束半径w(z)为光强降为峰值的1/e2 (≈ 13.5%)时距光轴的距离。孔径半径为w时可以透射约86.5%的光功率。如果孔径半径为1.5w或者2w，传输比例分别提高到 98.9%和99.97%。 

除了强度可以采用高斯方程描述，高斯光束的横向相位曲线可由最多二阶多项式来描述。在一个方向上相位的线性变化可由一个倾角描述，相位的二阶变化则与光束的发散和会聚相关。 

目录

1. 高斯光束的传输
2. 复数参数
3. 像散光束
4. 高斯光束和谐振腔模式
5. 高斯光束的重要性

高斯光束的传输 

通常在傍轴近似适用的情况下将光束看做高斯光束，即光束发散角比较小。这一近似下，传播方程中的二阶导数项可以忽略，只得到一阶微分方程。并且采用这种近似时，高斯光束在自由空间中传播仍然保持高斯型，其参数会发生一些变化。一束单色光束，波长为 λ，在z轴传播时，电场的复振幅为： 

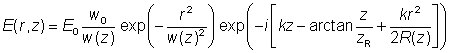
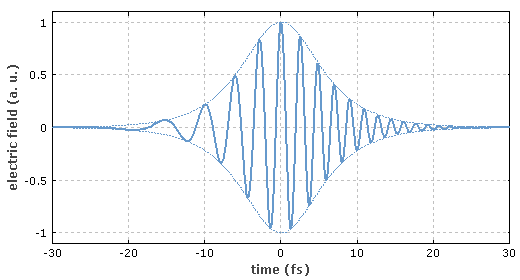
最大幅值为|E0|，束腰处的光束半径为 w0，波数 k = 2π / λ，zR为瑞利长度，波前的曲率半径为R(z)。震荡的实数电场可以通过乘以相位因子exp(i 2π c t / λ) 并且取实部得到。 

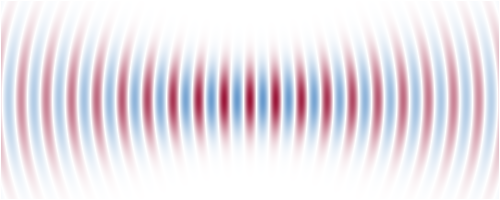
图1：高斯光束焦点处的电场分布。这时光束半径比波长稍大，光速发散角很大。根据以上方程，场由左侧向右侧移动。 

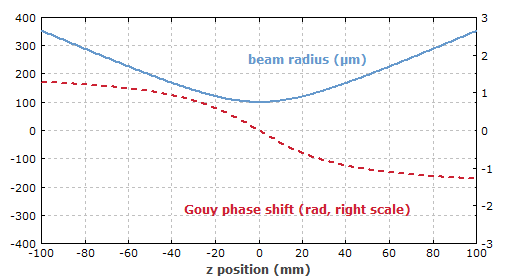
在传播方向上的光束半径变化为： 

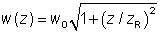
其中瑞利长度为： 

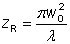
决定了在多长距离范围内光束不会发散很严重的传播。（之前通常采用共焦长b描述，它是瑞利长度的二倍。）准直光束（光束半径接近于常数）的瑞利长度与传播距离相比比较大。 

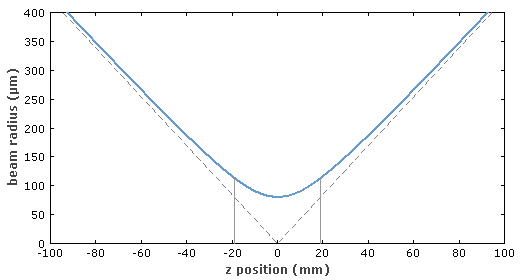
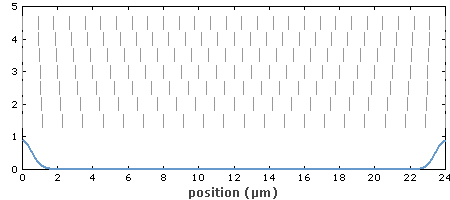
图2：高斯光束的光束半径变化（蓝色曲线）。两条竖线代表瑞利长度，虚线表明远离束腰的渐变变化情况。 

以上方程中 z = 0对应于束腰或者焦点，在该点光束半径是最小的，相位曲线是平坦的。波前曲率半径为R的演化遵循方程： 

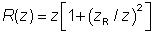
在透明介质中传播时，λ是介质中的波长（非真空波长）。上面采用的其它参数和方程都不用改变，这时假设了介质是各向同性、均匀和无损耗的。 

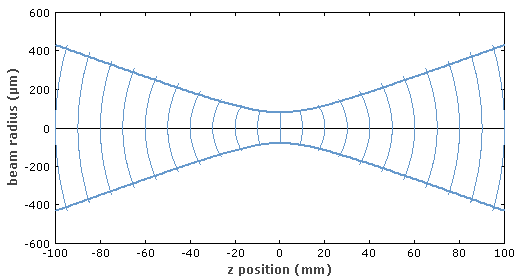
图3：具有弯曲波前的高斯光束。在接近于焦点和远离焦点时曲率都很小。 电场中的反正切项对应的是古依相移，对于光学谐振腔的谐振频率非常重要。 

远场的光束发散角为： 

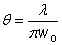
表明束腰半径越小，波长越长，则远离束腰后光束的发散越强。高斯光束的光束参数乘积（束腰半径与远场发散角的乘积）等于 λ/π，只与波长有关。如果激光光束的光束质量是非理想的，该值会更大。 

傍轴近似需要焦点处光束半径比波长大。这表明这时光束发散角不会很大，并且瑞利长度远大于光束半径。紧聚焦光束一般不能很好的满足傍轴近似，这时需要更加复杂的方法来计算光束传播情况。 

复数参数 

在z处高斯光束的状态可以由一个复数q表征： 

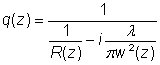
这样复电场可写为： 

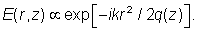
传输一定距离可以简单的表示为该距离上q参数的增加。当高斯光束通过一个曲面镜或者透镜时， q参数变化可由ABCD矩阵表示： 

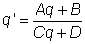
像散光束 

在两垂直的横平面方向上，写为x和y方向，高斯光束的半径和发散角可能不同。上面给出的方程可分别用来描述每一方向上光束半径的变化。如果两个方向上的焦点位置不重合，就称该光束是像散的。 

高斯光束和谐振腔模式 

如果谐振腔是稳定的，谐振腔中的光学介质是各项同性的，介质表面要么是平坦的或者是抛物线形状的，那么光学谐振腔横向的最低阶模式（TEM00或者横向基模）就是高斯模。因此，只辐射横向基模的激光器辐射的光束接近于高斯型。而任何偏离之前描述的条件，例如，增益介质中存在热透镜效应等，都会使光束为非高斯型，同时还会激发多个纵模。更高阶纵模可由厄米-高斯方程或者拉盖尔-高斯方程来描述。任意情况下，与高斯谱型的偏离都可以由 M2因子定量表示。高斯光束具有最高的光束质量，对应的光束参量乘积最小，并且对应的M2 = 1。 

光纤的基模并不严格为高斯型，但是形状与高斯型差别不是很大。因此，采用合适的光学元件，高斯光束可以有效进入单模光纤中（80%或更大）。 

高斯光束的重要性 

高斯光束的重要性体现在以下几个重要特性上： 

1. 在光轴的任意位置处高斯光束的强度横断面曲线都是高斯型，只是光束半径会发生变化。 
2. 通过一些简单的光学元件后（例如，无象差透镜）。 
3. 当腔内不存在光束畸变的情况下，高斯光束为光学谐振腔的最低阶模式（谐振腔模式）。因此许多激光器的输出都是高斯光束。 
4. 单模光纤中的模式形状接近于高斯型。通常在计算中会采用高斯近似因为这在计算光束传播情况时相对简单。 
5. 高阶模式对应的是厄米-高斯型。场分布更加复杂，光束参量乘积更大。 
6. 高斯模式分析可以推广到光束质量差的光束中，需要采用M2因子。